research

My research aims to quantify and understand the behavior and uncertainty of complex systems to enable safe, automated decision making. Specifically, I am interested in statistical verification of autonomous systems, including the derivation of probabilistic bounds for the correctness of learning or decision-making algorithms (see figure below). As automated decision making is integrated into safety-critical systems, engineers and regulators must provide quantitative guarantees, not just empirical evidence, to certify these technologies for safe and efficient real-world deployment. Probabilistic guarantees provide the rigorous evidence needed to ensure safe system behavior and meet certification standards, even under rare or unexpected conditions --- a prominent method for achieving this is reachability analysis.

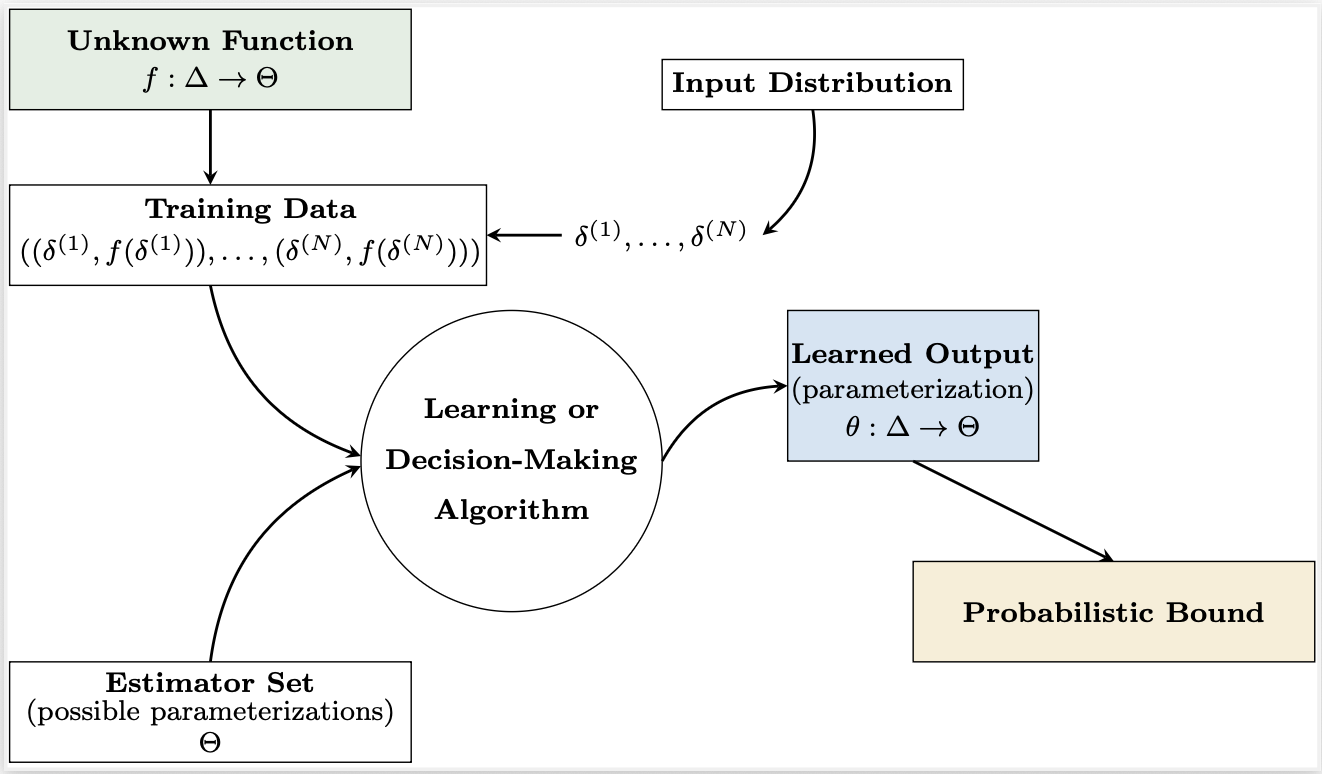
I focus on probabilistically capturing the behavior, uncertainty, and risk of systems in dynamic environments through (1) data-driven reachability analysis and (2) probabilistic risk frameworks, for use in monitoring and verification. My research represents a key step in achieving risk-aware, safe decision making for autonomous agents by understanding and bounding unknown system behavior in a tractable and interpretable manner.

Data-Driven Reachability Analysis

Data-driven reachability analysis relies on simulation or experimentation to learn probabilistically bounded sets directly from data. It can be utilized across applications, such as safe motion planning and collision avoidance, or software verification and bug detection. However, to achieve meaningful probability bounds, the amount of required data remains too high for real-time applications. My research aims to address this problem by estimating tight reachable sets with probabilistic guarantees, while minimizing computational and sample complexity.

Probabilistic Risk Frameworks

Real-world systems must adhere to nuanced safety and performance requirements while accounting for various forms of uncertainty and risk. For instance, imagine a surface vessel performing evasion maneuvers while subject to wave and wind disturbances. To accurately conduct motion planning, the vessel must have the ability to estimate environmental uncertainty, account for various sources of risk (e.g., stationary obstacles, other traffic participants, shallow waters, etc.), and comply with requirements originating in natural language (e.g., "maintain a safe distance from all other vessels" or "maintain a safe speed"). Signal temporal logic offers a flexible framework to encode and measure such natural language requirements in a mathematically rigorous manner. However, standard signal temporal logic does not offer means to incorporate uncertainty and only monitors one form of risk at a time. Therefore, my research aims to mitigate this gap by uniting risk estimation, reachability analysis, and uncertainty quantification.